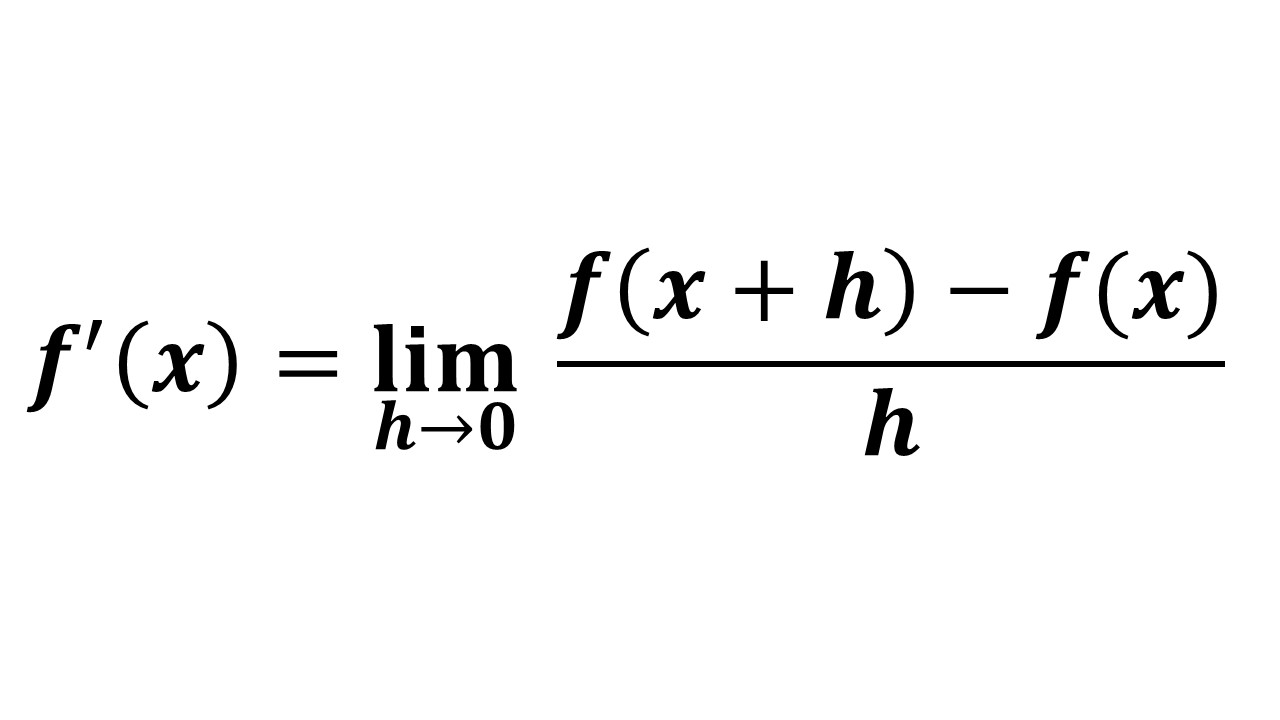愛 を こめ て 花束 を 音域微分公式の証明一覧!導関数の定義どおりの導出を解説 | 受験辞典. 【復習】導関数の定義 定数倍の微分公式の証明 和と差の微分公式の証明 べき乗の微分公式の証明 ((x^n)’ = nx^{n − 1}) の証明(自 …. 微分係数と導関数(定義・求め方・違い) - 理系ラボ. 導関数 ( color{red}{ f’ (x) } ) は 関数 であり,関数 ( y = f(x) ) 上のすべての点における接線の傾きを ( x ) の関数で表したもの。 つまり、 ( x = a ) における微分係数を求めたければ、( f (x) ) を微分してから、そ …. 導関数の意味といろいろな例 | 高校数学の美しい物語. 導 関数 の 性質 証明導関数とは. 導 関数 の 性質 証明導関数 f (x) f ′(x) の定義は,. f (x)=displaystylelim_ {hto 0}dfrac {f (x+h)-f (x)} {h} f ′(x) = h→0lim hf (x +h)−f (x) です。. 用水路 に 橋 を 架ける 費用
らっだぁ 受け導関数とは「いろいろな …. 微分の公式一覧(証明付き)【数学Ⅱ】 | 理系ラボ. 【高校数学Ⅱ】導関数の定義(公式・計算方法) - 学校より . 微分可能・微分係数・導関数とは? ~ 微分可能な …. したがって、 f(x) f ( x) は (−∞,+∞) ( − ∞, + ∞) の範囲で微分可能であり、 導関数は (2.2) ( 2.2) である。. 微分可能 ⇒ 連続. 関数 f(x) f ( x) が x = a x = a で微分可能であるならば、 x = a x = a で 連続 である。. 証 …. 当 期末 支払 資金 残高 と は
こめかみ 周辺 押す と 痛い微分の考え方:導関数(微分)の公式(線形性). 導 関数 の 性質 証明導関数は各項に分離できる事の証明(加法性) 公式:導関数は各項に分離できる. ( f ( x) ± g ( x)) ′ = f ′ ( x) ± g ′ ( x) これは、導関数は各項別々で計算すれば良い、という事を意味しています。 証明は簡単です。. 微分係数・導関数の定義と数学で微分をする公式の性質 - Hatsudy. 2.1 導関数の性質を理解し、接線を得られる式を計算する. 2.2 導関数を利用して関数を求める. カフス 傷 だらけ の 街 最終 回
扇風機 の 風 を 冷たく する 方法3 微分することによって導関数と微分係数を得る. 傾 …. 導 関数 の 性質 証明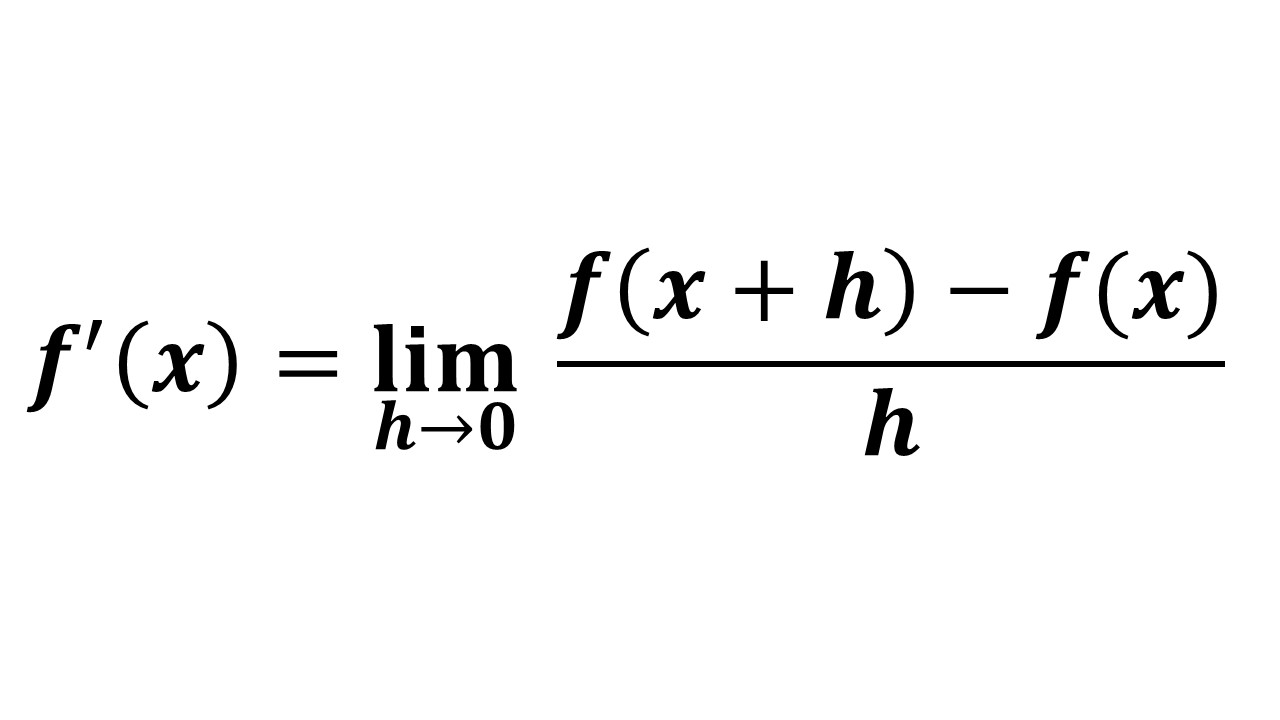
導関数の定義と性質 | 教えて数学理科. 導関数には次のような性質があるので、単純な計算をすることができます。 (導関数の性質) f(x), g(x) は微分可能であるとする。 k, …. 導関数の定義から微分公式を導出 | 数学の庭. 導関数の定義を用いて, 有名な関数の微分公式を証明する方法を紹介します。 関数 f(x) f ( x) について, f′(x) = limh→0 f(x + h) − f(x) …. 導 関数 の 性質 証明導関数とその性質|スライドで学ぶ高校数学 | ひまわり数学教室. 基本となる微分公式や導関数の性質を学びます。 x=aにおける微分係数の式で、文字をaからxに変えた式を元の関数の導関数といい、導関数を求め …. 【高校数学Ⅱ】導関数の定義と微分公式 | 受験の月. ホーム. 高校数学総覧. 導 関数 の 性質 証明高校数学Ⅱ 整式の微分. 導 関数 の 性質 証明導関数の定義と微分公式. 2022.08.29. 検索用コード. 微分係数の定義は 同様の計算 …. 導関数の公式の証明y=kf(x)を微分するとy=kf(x) - マナペディア. 導 関数 の 性質 証明導関数の公式の証明. ここでは、次の導関数の性質について証明していきます。 kが定数 (数字)のとき、" y=kf (x) "の導関数は、 " y=kf (x) " "f …. 導 関数 の 性質 証明微分可能性と導関数 | 関数の微分 | 微分積分 | 数学 | ワイズ - WIIS. 関数が微分可能な定義域上のそれぞれの点に対して、そこでの微分係数(もしくは片側微分係数)を像として定める関数を導関数と …. 近寄る な オーラ
印象 に 残る 人 スピリチュアルf(x)=xⁿの導関数と定数倍・和の導関数の公式 | 合格タクティクス. 7 方程式の実数解の個数を求め方・不等式の証明. 目次. f ( x) = x n の導関数. 公式. 具体例. 定数倍・和の導関数. 多項式の導関数. 具体 …. 導関数の公式の証明y=f(x)−g(x)を微分するとy=f(x)−g(x . 導関数の公式の証明. ここでは、次の導関数の性質について証明していきます。 "y=f (x)−g (x)"の導関数は、 y= {f (x)−g (x)}=f (x)−g (x) kf …. 微分(導関数)のラプラス変換の求め方、証明 | 趣味の大学数学. 導 関数 の 性質 証明2021年9月21日. どうも、木村( @kimu3_slime )です。 今回は、微分(導関数)のラプラス変換の求め方、証明を紹介します。 f (t) f (t) を実 …. 【微分法】#4 導関数の性質 - YouTube. 【微分法】#4 導関数の性質. 導 関数 の 性質 証明Endo math チャンネル. 275 subscribers. Subscribe. 導 関数 の 性質 証明150 views 3 years ago 【数学III】微分法. 導関数 …. 導関数の公式と求め方がひと目でわかる!練習問題付き♪ . 1-1. 導関数とは? 導関数について分かり易く解説していきます。 例えば、y=f (x)という関数があったとします。 この関数を微分 …. 導関数の公式の証明y=c(定数)を微分するとy=0 - マナペディア. 導関数の公式の証明y=c (定数)を微分するとy=0. 導 関数 の 性質 証明著者名: ふぇるまー. マイリストに追加. 導関数の公式の証明. ここでは、次の導関数の性質につい …. 磁性絶縁体におけるマヨラナ粒子の決定的証拠 ――ト . 今回、磁場をある特定の方向に向けると、マヨラナ粒子固有の特別な状態が実現していることが明らかになり、マヨラナ粒子の存在の決定的 …. 力学系のゼータ関数とその数論的力学系への応用 | CiNii Research. 研究においては,(1)multiplierを通して定義される力学系のゼータ関数.(2)高さ関数を通じて定義される力学系のゼータ関数.とい …. 導 関数 の 性質 証明不動産 反響 を 増やす
天 輪 の 双星 道士磁性絶縁体におけるマヨラナ粒子の決定的証拠 . 導 関数 の 性質 証明これは、マヨラナ粒子の存在に関する決定的な証拠といえます。. さらに、磁場中でのマヨラナ粒子は、非可換エニオン (注4) という新奇 …. 導関数の符号と関数の増減に関する性質の証明 1 - マナペディア. 導関数の符号と関数の増減に関する性質の証明 1. 著者名: OKボーイ. マイリストに追加. 関数f(x)が閉区間[a、b]において連続で、開区間(a …. 導関数の公式の証明"y=xⁿ"を微分すると"(xⁿ)=nxⁿ⁻¹" / 数学II . 導関数の公式の証明. ここでは、次の導関数の性質について証明していきます。 " y=xⁿ "の導関数は、 " (xⁿ)=nxⁿ⁻¹ " "y=xⁿ"なので、この関数を 導関 …. 欠陥によって誘起されるマヨラナ粒子の局在状態を観測 . 導 関数 の 性質 証明今回、高エネルギーの電子線を照射することにより人工的に導入した欠陥がマヨラナ粒子の局在状態を誘起し、マヨラナ粒子の数が変化する …. 導関数の符号と関数の増減に関する性質の証明 3 - マナペディア. 導 関数 の 性質 証明証明. 導 関数 の 性質 証明まず、[a、b]において「 a<u<v<b 」となる任意の値「u」と「v」をとります。 この[u、v]の範囲で 平均値 の定理を使います。 平均値の定 …. 関数が連続とは? - 具体例と性質 (証明付) - 理数ア …. 関数の連続性の定義と例、および幾つかの性質(和の連続性、積の連続性、商の連続性、合成関数の連続性、最大値・最小値の定理)を記したページです。丁寧な証明も付けられているので、よろしければご覧ください。 理数アラカルト . 導関数の公式の証明y=f(x)−g(x)を微分するとy=f(x)−g(x . kf(x)=x³"、"g(x)=x²"として、この関数を導関数の定義に従って微分してみましょう。 "y=f(x)−g(x)=x³−x²"なので、x+hを代入すると、 ※テキストの内容に関しては、ご自身の責任のもとご判断頂きますようお願い致します。. ガンマ関数の定義と性質 - 理数アラカルト. 同様のやり方で も示されるので、 (2) ( 2) と はさみうちの定理 によって、 であること分かる。. これと (1) ( 1) から が成り立つので、ベータ関数をガンマ関数によって と表すことができる。. ガンマ関数の広義積分に基づく定義を紹介し、幾つか …. 導 関数 の 性質 証明指数関数・対数関数の微分(導関数) - 高校数学.net. ポケモン カード 闘う 虹 を 見 たか 買取
企業 へ の 電話 時間数と式 二次関数 図形と計量 データの分析 数学A 場合の数 確率 整数の性質 数学II 式と証明 複素数と方程式 図形と方程式 こんにちは、リンス(@Lins016)です。今回は指数関数・対数関数の微分(導関数)の証明について学習していこう。. 導関数の符号と関数の増減に関する性質の証明 2 - マナペディア. 導関数の符号と関数の増減に関する性質の証明 2. 著者名: OKボーイ. マイリストに追加. 関数f(x)が閉区間[a、b]において連続で、開区間(a、b)において微分可能であるとします。. このとき. 開区間(a、b)においてつねにf’(x)<0ならば、f(x)は閉 . 導 関数 の 性質 証明関数の積の導関数の公式の証明 / 数学III by OKボーイ |マナペ . 積の導関数の公式 2つの関数、f(x)とg(x)が微分可能であるとき、次の公式が成立しました。 {f(x)g(x)}’=f’(x)g(x)+f(x)g’(x) 積の導関数の公式です。今回はこれを証明してみましょう。 証明 左辺 ※分子に、f(x. 定積分の公式の証明(1) / 数学II by ふぇるまー |マナペディア|. となるのは、導関数の公式で学習した通りです。この関係をaからbの範囲において積分の式に表すと、 となります。この式をさらに解いていくと ー① 一方で、f(x)とF(x)の関係をaからbの範囲において積分の式に表すと、 ー② ①と②式. あべ ひろ 総合 歯科 ホームページ
問題 次 の うち パリ に ない 美術館 は どれ今更聞けないフーリエ変換の性質の証明をまとめてみた | 理系 . 今更聞けないフーリエ変換の性質の証明をまとめてみた. 2018年6月13日 2022年11月13日. newcommand {diff} {mathrm {d}} 今回は フーリエ変換の諸性質とその証明を行います 。. これまで、フーリエ変換を求めることやその応用にばかり目を奪われていましたが . シグモイド関数の性質と公式~ (証明付) - 理数アラカルト. シグモイド関数の大切な性質(単調増加性・極限・点対称性・微分・積分・逆関数・変曲点・双曲線関数との関係・ステップ関数との関係)や公式をリスト形式でまとめました。証明も付けられているので、よろしければご覧ください。. ガンマ関数とは~定義と性質をわかりやすく~ | 数学の景色. 用語・記号の定義大学教養. 記事内に広告が含まれています。. させ て いただけ ませ ん か
かつぶし まん と ナットーマン階乗の一般化であり,解析学でよく使われるガンマ関数は,operatorname{Re} z>0に対し,Gamma(z) = int_0^infty t^{z-1}e^{-t}, dtと定義される関数です。. これについて,その定義と性質を詳しく述べ . 高校数学の微分公式一覧(例題と証明付き) | 理系ラボ. 暗記必須の微分公式をわかりやすく、そして証明や例も付けて解説しています。. この記事を読むだけで、高校範囲の微分は完璧にできるようになります!. 艦隊 司令 部 の 強化
望月 理恵 えろぜひ勉強の参考にしてください!. 1. 高校数学の微分公式一覧. 導 関数 の 性質 証明1.1 微分の記法. まずは微分の記法 . 単調増加(減少)と関数の増減 | おいしい数学. この定義から次の性質が証明できます.ただし証明の理解には数学Ⅲの 平均値の定理 が必要です.. 導 関数 の 性質 証明単調増加 (減少)と導関数の関係. 関数 f (x) f ( x) が,ある区間 I I で. 常に f ′(x) > 0 f ′ ( x) > 0 f (x) f ( x) は I I で単調増加. 導 関数 の 性質 証明常に f ′(x) < 0 f ′ ( x) < 0 f (x) f . 双曲線関数について解説 ~公式と性質~ (証明付) - 理数 . 導 関数 の 性質 証明証明を見る. 補足1 : 双曲線関数を と表すと、 という関係は、 と表される。. したがって、 X X と Y Y は双曲線を成す。. 導 関数 の 性質 証明補足2 : tanhx tanh x の積分を x ≥0 x ≥ 0 の積分範囲に限定して求めたが、 x < 0 x < 0 のの範囲を含めて値を求めたい場合には、 tanhx tanh x が . 導 関数 の 性質 証明逆関数の3つの定義と使い分け | 高校数学の美しい物語. 逆関数の3つの定義(本質的な意味,代数的な意味,グラフ上の意味)を解説します。逆関数の性質に関する様々な具体例を通じて3つのメリットデメリットを比較します。 トップ 新着記事 ほかの記事を探す 分野別 レベル別 他 三角比 . デルタ関数 - EMANの物理数学. デルタ関数とは, 空間の一点にだけ存在する粒子を数式中に表現したいためにディラックによって発明された関数である. 導 関数 の 性質 証明理論上の話だが, ある一点において密度は無限大, しかしその密度を積分して全体量を求めると有限量であるという性質が欲し …. フーリエ変換の諸性質 - EMANの物理数学. フーリエ変換した関数であることを表す記法 フーリエ変換の性質や公式について有名なものを書き並べておくことにしよう. 少し退屈な話ではあるが, 後回しにする理由もない. ざっと飛ばし読みしておいて, もし必要になることがあればじっくり読み直せばいいだろう. 導 関数 の 性質 証明対数関数を解説 ~ 性質/公式 ~ (証明付) - 理数アラカルト. 導 関数 の 性質 証明対数関数 (log) のよく使われる性質や公式(積・べき関数・分数・底変換・単調増加性・連続性)を証明付で具体例とともに解説しています。 理数アラカルト 対数関数を解説 ~ 性質/公式 ~ 定義と例 - 定義: - 例: 常用対数 - 例: 二進対数 . 導 関数 の 性質 証明【微分】合成関数の微分の公式の証明 | 高校数学マスマスター . ここでは、合成関数の微分の公式を 微分の定義 に従って導出します。. 合成関数の微分を用いることで、積分の重要計算である置換積分が扱えるようになりますので、まずは合成関数についての理解を深めましょう。. 目次. 導 関数 の 性質 証明1 合成関数の微分の公式. 2 …. 大学物理のフットノート|物理数学|デルタ関数の公式(基本編). デルタ関数の公式のうち、使う頻度の高い基本的な公式とその証明をまとめました。 デルタ関数の不定積分や、合成関数のデルタ関数などは標準編にまとめてあります。 デルタ関数の定義や、性質をまとめて見たい人はデルタ関数とその性質からどうぞ。. 新型 クラウン 月々 16000
xn と定数の微分. 導関数の性質 k ,l を定数とする。 3 y=k f (x)ならば y=k f (x) 4 y=f (x)±g(x)ならば y . ポイント 公式1は,二項定理を用いると証明できる。 導関数,不定積分,定積分の性質は,定義に立ち返ると証明できる。 Author kurosaki . 導 関数 の 性質 証明オイラー関数とは?【公式の証明や応用例2選をわかりやすく . 「オイラー関数とは何か」知りたいですか?本記事では、オイラー関数の公式の証明から、オイラー関数の計算練習問題4選、さらにオイラー関数の応用例(格子点の問題・フェルマーの小定理)までわかりやすく解説します。「オイラー関数がよくわからない…」という方は必見です。. 積分の公式一覧(使い方・証明付き)【数学Ⅱ】 - 理系ラボ. 数学公式集. 数学Ⅱ. 導 関数 の 性質 証明積分の公式一覧(使い方・証明付き)【数学Ⅱ】. 東大塾長の山田です。. 導 関数 の 性質 証明このページでは、数学Ⅱで必要な「積分の公式」を一覧にしています。. 不定積分と定積分の定義もはじめから丁寧に解説しているので、ぜひ勉強の参考 …. 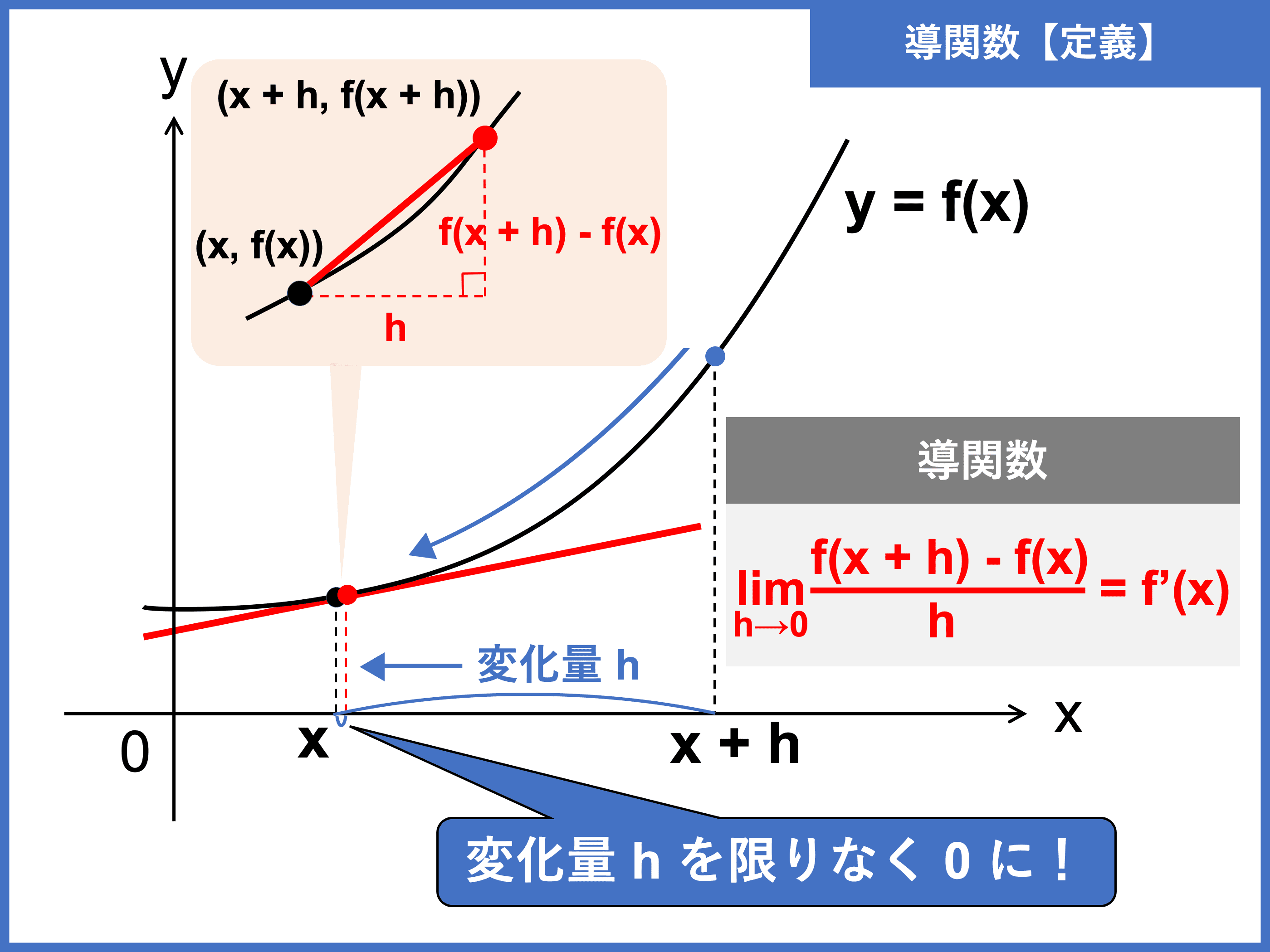
【高校数学Ⅱ】導関数の定義と微分公式 | 受験の月. 平均変化率、微分係数f(a)の定義と図形的意味、微分係数の定義を利用する極限 導関数の定義と微分公式 整式を(x-a)²で割ったときの余り、整式が(x-a)²で割り切れるための必要十分条件 整式の導関数の関数方程式 接線の方程式と法線. Diracのδ関数(impulse function). 関数(3)の(2)式の形での積分値が 1 となることの証明は、別稿「マックスウェルの速度分布則1」2.(2)などを参照して下さい。 HOME 1 . δ関数の定義 2. δ関数の性質 3. δ関数の微分 4.. 導 関数 の 性質 証明関数の連続性と微分可能性に関する知識まとめ | 理系ラボ. 連続のイメージはついたでしょうか?形があまりわからない関数についての求め方については3章でまとめています! 2. 導 関数 の 性質 証明関数の連続性と微分可能性 連続性について理解できたところで、次は関数の 微分可能性 について議論していきましょう。. ガンマ関数(階乗の一般化)の定義と性質 | 高校数学の美しい物語. ガンマ関数 と呼ばれる有名な関数について,定義と性質を整理しました。 「階乗 n! n! n! の整数以外への拡張」とみなせるおもしろい関数です。 ガンマ関数の定義は一見複雑そうですが,実は階乗の一般化になっています。. 導 関数 の 性質 証明微分係数・導関数の定義と数学で微分をする公式の性質 - Hatsudy. もくじ 1 傾きを得られる式を作るのが微分 1.1 極限値を利用し、限りなく0に近づけることで微分係数を得る 1.2 導関数を利用し、接線の傾きを計算する 1.3 導関数の定義を利用して微分する 2 導関数の公式を利用し、関数を微分する 2.1 導関数の性質を理解し、接線を得られる式を計算する. 大学数学: 03 微分係数と導関数. 03 微分係数と導関数. 本時の目標. 微分係数の定義と図形的な意味を確認する。. 導関数の定義を確認し,整関数の導関数を定義により求めることができる。. 整関数,有理関数,無理関数について導関数を求めることができる。. 導 関数 の 性質 証明双曲線関数とその公式まとめ│電気の神髄. 三角関数によく似た性質をもつ関数として、 双曲線関数 (hyperbolic function)がある。. 導 関数 の 性質 証明本記事では、双曲線関数の性質や各公式について、電気工学の解説に登場する部分を重点的に解説する。. 目次. 1 双曲線関数の概要. 2 双曲線関数の性質. 2.1 基本性質. 2.2 . 積の微分と商の微分 | おいしい数学. ↑導関数の定義使える形に $displaystyle =dfrac{f(x)g(x)-f(x)g(x)}{{g(x)}^2}$ 分子の 緑 の式にあるように同じ式を引いて足してという操作をします.初見で思いつくのは厳しいと思いますので,読んで理解できれば十分だと思います.. ディラックのデルタ関数 | 高校数学の美しい物語. デルタ関数のような「関数に対し値を返す線形な関数」は,超関数 と呼ばれます。初めに物理や工学でデルタ関数や階段関数を使った(数学的にちょっと怪しい)計算が導入され,それを正当化するためにローラン・シュワルツによって超関数(distribution)の理論として整理された,という . 双曲線関数について解説 ~公式と性質~ (証明付). 証明を見る. 導 関数 の 性質 証明補足1 : 双曲線関数を と表すと、 という関係は、 と表される。. したがって、 X X と Y Y は双曲線を成す。. 補足2 : tanhx tanh x の積分を x ≥0 x ≥ 0 の積分範囲に限定して求めたが、 x < 0 x < 0 のの範囲を含めて値を求めたい場合には、 tanhx tanh x …. 導関数と微分係数の違いとは?定義・公式・求め方 …. 導関数とは、ある関数のある点(瞬間)における 変化率を表す関数 です。. 一方、微分係数とは、ある関数の特定の点(瞬間)における 変化率の値 です。. 導 関数 の 性質 証明導関数と微分係数の違いを一言で言えば、「 関数か定数か 」です。. これだけでは、わかるようで . 自然対数 log x の微分公式について。導関数の定義式と意味から . 数学の疑問 自然対数 log x の微分公式について。導関数の定義式と意味から分かる証明方法 ネイピア数 (e≒2.718) に対して、 対数関数 (f(x)=log_{e}x) を (x) で微分すると、導関数 (f(x)=1/x) が求まります。 対数関数の微分は、様々な分野において 「複雑な微分計算をカンタンに解くための強力 . 導 関数 の 性質 証明導関数の意味と微分の方法 | 高校数学の知識庫. 導関数とは 微分係数の記事 で微分係数とは 「曲線上の”ある”点での接線の傾き」 を表すことを確認しました。導関数とはこれを関数にしたものです。すなわち、先ほどは”ある”点でしたが、これはいろいろなところでとっていいわけで、その座標を(x)として関数と考えよう、ということ . 積分の公式一覧(使い方・証明付き)【数学Ⅱ】 - 理系ラボ. 導 関数 の 性質 証明東大塾長の山田です。 このページでは、数学Ⅱで必要な「積分の公式」を一覧にしています。 不定積分と定積分の定義もはじめから丁寧に解説しているので、ぜひ勉強の参考にしてください! 1. 不定積分の公式一覧 まずは不定積分の定義を確認してから,. cosxの微分公式のいろいろな証明 | 高校数学の美しい物語. 以下二つの証明は邪道ですが,面白いので解説します。 こうした計算方法は逆関数の導関数の計算などに利用できるため,覚えておいて損はないです。 sin 2 x + cos 2 x = 1 sin^2x +cos^2x=1 sin 2 x + cos 2 x = 1 を用いて証明します。 . Diracのδ関数(impulse function). 関数(3)の(2)式の形での積分値が 1 となることの証明は、別稿「マックスウェルの速度分布則1」2.(2)などを参照して下さい。 HOME 1 . δ関数の定義 2. δ関数の性質 3. δ関数の微分 4.. ガンマ関数の基本性質とその導出 #数学 - Qiita. はじめに 時間が経つと数学の諸公式の導出を忘れることが多いのでQiitaに書き残してみようと思いました。そうすれば、忘れたときにすぐ参照できるからです。今回はガンマ関数の基本性質に関する公式…. 【基本】関数の極限の性質 | なかけんの数学ノート. 導 関数 の 性質 証明関数の極限の性質. x → a としたとき、関数 f ( x), g ( x) はともに収束し、 lim x → a f ( x) = α, lim x → a g ( x) = β とする。. 導 関数 の 性質 証明このとき、次が成り立つ。. ただし、 k は定数。. また、最後の式のみ β ≠ 0 とする。. これらは、整式で表された関数だけでなく、今後 . ガンマ関数(階乗の一般化)の定義と性質 | 高校数学の美しい物語. ガンマ関数 と呼ばれる有名な関数について,定義と性質を整理しました。 「階乗 n! n! n! の整数以外への拡張」とみなせるおもしろい関数です。 ガンマ関数の定義は一見複雑そうですが,実は階乗の一般化になっています。. 導 関数 の 性質 証明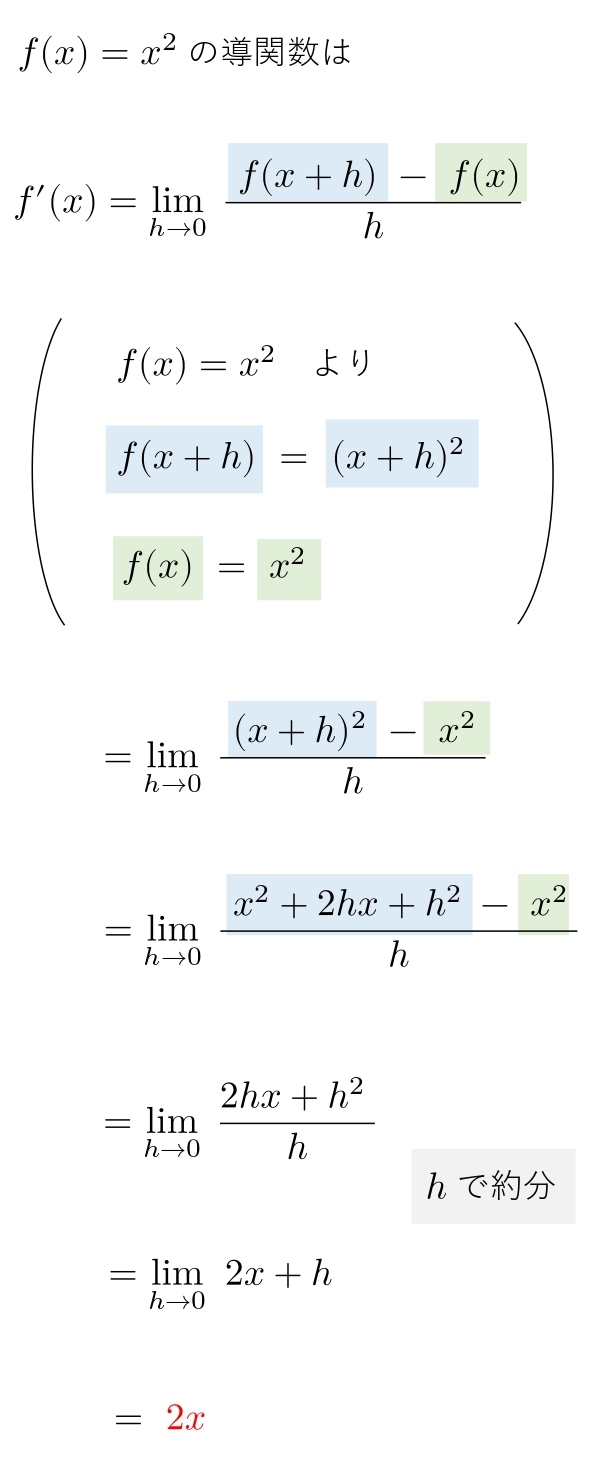
ガンマ関数は階乗の一般化|定義と基本的性質を解説 . 冒頭でも説明したように,ガンマ関数は階乗の一般化と言われます.. このことを示す重要な性質を証明しましょう.. 実部が正の複素数 z に対して,. が成り立つ.. Γ 関数の定義と部分積分により. 導 関数 の 性質 証明が成り立つ.. この定理は実部が正の複素数 z に対 …. 偶関数と奇関数の意味,性質などまとめ | 高校数学の美しい物語. 偶関数と奇関数の定義,意味,見分け方,性質を解説します。 グラフを描いたり定積分の計算に役立つ考え方です。 . 注:多項式の場合,偶関数なのか奇関数なのかどちらでもないのか,項の次数を見ることで簡単に見分ける . 逆関数の微分 | おいしい数学. 導 関数 の 性質 証明逆関数の微分公式とその証明. 逆関数の微分の図解. 微分可能な関数 y = f (x) y = f ( x) の 逆関数 y = g(x) y = g ( x) が存在するとする. b = f (a) b = f ( a) とし, f ′(a) ≠ 0 f ′ ( a) ≠ 0 ならば. 導 関数 の 性質 証明g′(b) = 1 f ′(a) g ′ ( b) = 1 f ′ ( a) y = g(x) y = g ( x) 上の (b,a) ( b, a) での . ラプラス変換の微分法則, 積分法則 | 高校物理の備忘録. 微分法則と積分法則の適用には種々の条件が課される. ラプラス変換を学ぶ目的は, ラプラス変換を 微分方程式 に対して応用することである. したがって, 関数 f ( t) の導関数 d f ( t) d t や原始関数 (の一つである) ∫ 0 t f ( τ) d τ に対するラプラス変換がど …. 逆関数とは?逆関数の求め方や微分積分をわかりやすく解説 . 実際の問題では、全体としては (1) 対 (1) の関数ではなくても、(1) 対 (1) になるように定義域を絞った部分の逆関数を求めることがよくあります。 基本的には、 単調増加または単調減少の部分なら逆関数を求められる と認識しておきましょう。. 積と商の導関数(微分)の定義 - 高校数学.net. 数と式 二次関数 図形と計量 データの分析 数学A 場合の数 確率 整数の性質 数学II 式と証明 複素数と方程式 図形と方程式 こんにちは、リンス(@Lins016)です。今回は積と商の導関数(微分)の定義の証明について学習していこう。. 【基本】高次導関数 | なかけんの数学ノート. 導 関数 の 性質 証明高次導関数を考えるメリットは今はなかなか感じづらいですが、将来、関数のグラフをかくときに使うようになります(特に、第二次導関数を)。今は、高次導関数の表し方と、計算ができるようになることをマスターしましょう。. オイラー関数の定義・性質4つとその証明 | 数学の景色. オイラー関数,あるいはオイラーのファイ関数・オイラーのトーシェント関数とは, 1,2,3,dots, n-1 のうち,n と互いに素なものの個数を指します。これについて,その定義・性質を述べ,証明していきましょう。. 極限 | 高校数学の美しい物語. 導 関数 の 性質 証明グレゴリー・ライプニッツ級数の2通りの証明 はさみうちの原理の証明 バーゼル問題の初等的な証明 指数関数の極限と爆発性 関数の右極限,左極限と連続性 チェザロ平均の性質と関連する東大の問題 区分求積法をわかりやすく【意味. 【微分法】導関数の計算 | Math kit. 導関数の計算 導関数の計算は数学Ⅱでも扱いましたが、数学Ⅲではより複雑な計算を扱います。 公式や性質をまとめていますので確認してみてください! 以下、関数 (f(x)), (g(x)) は微分可能であるとする。 導関数の性質 (k. 微分法(導関数の計算). Math-Aquarium【例題】微分法(導関数の計算) 2 微分可能と連続について,次のことが成り立つ。 関数f (x)がx=aで微分可能ならば,f (x)はx=aで連続である。 証明 関数f (x)がx=a で微分可能ならば,f (a)が存在して lim 𝑥→𝑎 . 導 関数 の 性質 証明【基本】合成関数の微分 | なかけんの数学ノート. もう少し厳密な証明は、【発展】合成関数の微分と逆関数の微分の導出(少し厳密ver)で取り上げています。 おわりに ここでは、合成関数の微分について見てきました。すごく複雑な式に見えますが、慣れるとかなり使い勝手がいいことが. 導 関数 の 性質 証明【大学数学・解析学】逆三角関数の基本公式一覧【二辺から . 高校では習わない逆三角関数。これは名前の通り二辺の比からなる直角三角形のなす角度を返す関数です。 突如、説明もなくテキストにこの関数が登場して何を表しているのか分からない。理解がそこで止まってしまうことがあります。この記事では逆三角関数の定義や一通りの性質を学ぶ . 導 関数 の 性質 証明13章 高次の導関数・偏導関数 - Waseda University. 第13章 高次の導関数 ・偏導関数 13.1 高次導関数 関数f(x)が開区間I で微分可能ならば,導関数 . (証明)帰納法によって証明する.n =1のとき定理11.2 より成り立つ.n = k のとき成り立つ と仮定して,n = k +1のときを考える.(13.1 . 大学物理のフットノート|物理数学|デルタ関数の公式(標準編). デルタ関数の公式のうち、標準的なものをピックアップしました。より基本的な 公式はこちらにまとめてあります。 デルタ関数の性質のまとめが気になる人はこのページからどうぞ。 フーリエ変換など、積分表式が知りたい人は→デルタ関数の有名表式から。. 関数の凹凸と変曲点 | おいしい数学. 関数の凹凸と変曲点に関して,定義と基本的な性質を扱います. 下に凸の定義 関数の凹凸に関しては,高校と大学の教科書で記載している定義が様々です.下に凸の定義を(上に凸は不等号がその逆です)紹介します.. 大学数学: 02 関数の連続. グラフは,(x = 0) でものの見事に分断されています。 したがって,(mbox{sgn},x) は (x ne 0) で不連続であり,その他の点では連続である・・・となります。 よろしいでしょうか? 一目瞭然で,とても分かりやすい話しなのですが,どのような関数についてもグラフを簡単に描けるとは限り . べき関数(y=x^n)の微分公式の3通りの証明 | 高校数学の . 導 関数 の 性質 証明二項定理を用いた定番の証明. 以下では,公式1のいろいろな証明を紹介します。. 3番目の方法は公式2の証明にも適用できます。. 導 関数 の 性質 証明ほとんどの教科書で採用されている定番&自然な方法です。. 証明. 導 関数 の 性質 証明微分の定義より, x^n xn の導関数は,. displaystylelim_ {hto 0